Workshop invited talk: Reliable Neural Operators: Error Control through Residual Correction and Beyond
Jun 24, 2025·
 ·
0 min read
·
0 min read
Prashant K. Jha
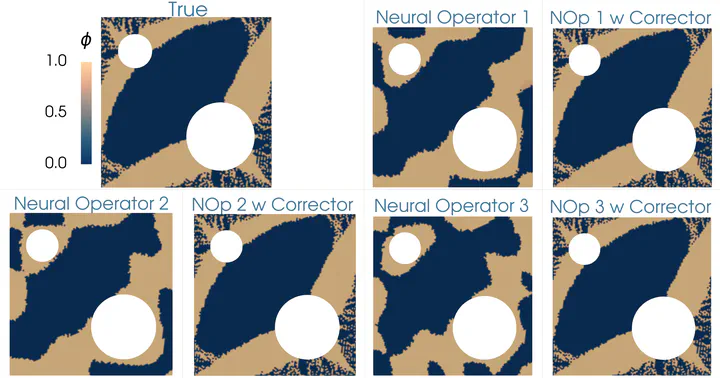 Topology Optimization of Diffusivity Field
Topology Optimization of Diffusivity Field
Abstract
Accurate surrogate models are crucial for advancing scientific machine learning, particularly for parametric partial differential equations. Neural operators provide a powerful framework for learning solution operators between function spaces; however, controlling and quantifying their errors remains a key challenge for downstream tasks, such as optimization and inference. This talk presents a residual-based approach for error estimation and correction of neural operators, thereby improving prediction accuracy without requiring retraining of the original network. Applications to Bayesian inverse problems and optimization are discussed. We will conclude by highlighting emerging ideas and recent progress aimed at enhancing the reliability of neural operators and opening new directions at the intersection of learning, adaptivity, and decision-making.
Date
Jun 24, 2025 12:00 AM
Event
Location
Montréal, Canada
1375 Avenue Thérèse-Lavoie-Roux, Montréal, QC H2V 0B3