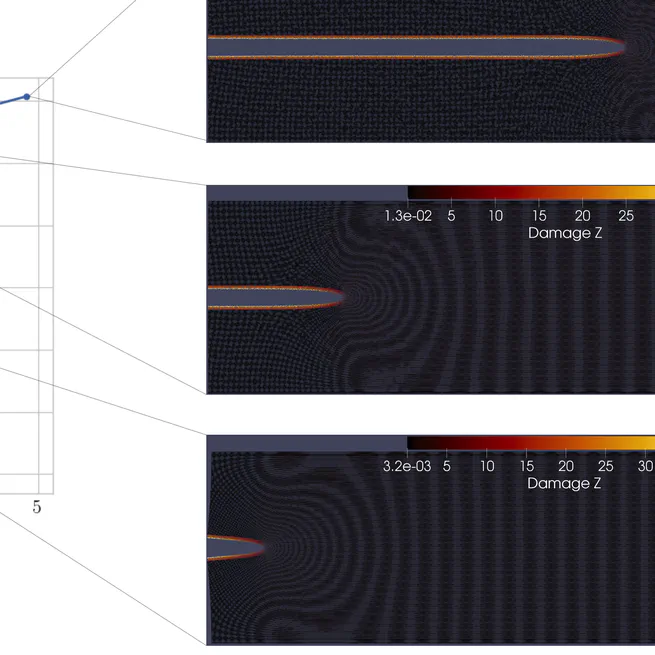
Analysis and application of peridynamics
Analysis and application of peridynamics
Jan 1, 2025
Nodal finite element approximation of peridynamics
In this work, nodal finite element discretization is detailed.
Mar 11, 2024
NLMech: Implementation of Finite Difference/Meshfree Discretization of Nonlocal Fracture Models
Sep 29, 2021
Peridynamics-Based Discrete Element Method (PeriDEM) Model of Granular Systems Involving Breakage of Arbitrarily Shaped Particles
Jun 1, 2021
Nonlocal Elastodynamics and Fracture
Mar 17, 2021
Finite Element Approximation of Nonlocal Dynamic Fracture Models
Mar 1, 2021
An Asynchronous and Task-Based Implementation of Peridynamics Utilizing HPX—the C++ Standard Library for Parallelism and Concurrency
Dec 4, 2020
Kinetic Relations and Local Energy Balance for LEFM from a Nonlocal Peridynamic Model
Nov 1, 2020
Finite Element Convergence for State-Based Peridynamic Fracture Models
Mar 1, 2020
Complex Fracture Nucleation and Evolution With Nonlocal Elastodynamics
Oct 1, 2019